さて突然ですが、円周率πの値が 3.14… となるのはなぜなのでしょうか。本当は 3.5とか3.75とか、あるいはちょうど3だったりするのでは？

今回はこれを検証するのがテーマです。当たり前と思われ、受け入れられていることを改めて自分自身で確かめてみることは案外面白いものです。ときにはギリシャの哲学者のように、暇すぎて考え事をせざるを得ないような贅沢で悠久の時を生きてみましょう。

前提: 私たちは大して賢くなかったんだ

今回のコラムでは前提として、以下のような制限を設けましょう。
・私たちはたいして賢くなく、難しいことはできない、わからない
・だけど手元にはパソコンがある
・パソコンの関数電卓はつかえない
ということにしましょう。
パソコン自体は大したスペックでなくても大丈夫ですが、スマホやタブレットはプログラミングに向かないのでやめましょう。もちろんChatGPTもダメです。

あともう一つ、制約をつけましょう。
難しいことはやらないので、したがって説明のできない公式を天下り的に使うこともやめましょう。
ちゃんと原始的な一人の人間として、紙とペンと算数とパソコンだけ（！？）を使って、円周率πの値を求めてみましょう。

そもそも円周率πとは？

なるべくわかりやすく話しますので過去何らかのトラウマを抱いている方も、何とかついてきてください。

さて、そもそも円周率πとは何なのでしょうか？
円周率は幼い頃に学んでいるので、割とそれをしっかりと覚えている人は少ないのではないでしょうか。かくいう私自身も物心がついた頃には円周率の勉強を終えていて、円の面積が半径 x 半径 x 3.14で求められる事だけが頭に残っていた印象です。（小学校の先生はちゃんと私に教えていてくれたのでしょうか？）

円周率3.14が出てくる公式といえば、円の面積の公式以外にも円周に関する公式があります。円周は直径 x 3.14で求められますね。
ふーん、まあなるほどという感じですが、実はここに重要なエッセンスが含まれています。

①円周 = 直径 x 3.14
②円の面積 = 半径 x 半径 x 3.14

と二つの公式が出てきましたが、公式とはいえ、①②の間には重要な違いがあります。

実は①円周の公式の方は、公式というよりも円周率の定義に近いものなのです。

円周率は直径と円周の長さの比のことである。

そうです。円周率とはそもそもが直径と円周の比を意味しているわけです。

そうなると
円周率 = 円周 ÷ 直径
と定義されるので、
円周 = 直径 x 円周率
となるのも当然ですね。
一応、公式と呼べるとは言え、これはほぼほぼ円周率の定義そのものと言ってもよい代物なのです。

それと比べると、②円の面積の公式は、直感的に即座に導出できるものではないので公式と呼ぶにふさわしいものです。

ちょっと大人の寄り道

ところで、上記の定義からするとやや気がかりなことがあります。
まるで円の大きさにかかわらず、円の半径と円周の比率は常にかわらずπという決まった値になるといった前提になっています。円周率πは円の大きさによって変わったりはしないのでしょうか？

これを説明するのには、互いに相似な図形については、任意の２か所の線の長さの比は互いに等しいということを示す必要があるのですが、ここだけは本日の約束を破って天下り知識として飛ばしてしまいましょう。

といいつつ、一応定性的に納得ができるよう一回だけ努力してみます。

例えばあなたの体が突如巨大化したと想像してみてください。
それでも両足の長さは大体一緒ですし、あるいは両手を広げると大体身長と同じになります。
そして何より素晴らしいのは、目と鼻と口のバランスも相変わらずバッチリですね！

こんな感じにね！

だから、たぶん円を縮小、拡大しても、直径と円周の比率はいつも変わらないであろうと、証明はできないもののほぼ確実にそうであろうなという予想がつきます。そう思いますよね？

そのようなわけで、円周率は必ず一定の値になるということで話を進めます。

とりあえず円周率を求めにかかろう

さあ、では円周と直径の比率を求めれば良いので、後は紙と鉛筆とコンパスと定規でも使ってみましょうか。
これで大体の長さの比率が分かりそうです。
ところがやり始めると分かりますが、困ったことに、定規ではまっすぐな線以外の測定ができません。

円を描き、円周をなぞるように紐を置きその長さを測ることで、恐らく円周率は3とか3.2とか、そのあたりかなくらいはわかると思います。

大体はそれでいいのですが、かつて円周率を３と近似するという噂話が出たことで、世の中から物凄く多くの怒りが噴出した事実を考えますに、我々はもう少しだけ、円周率の真の値に近づきたいと思っています。

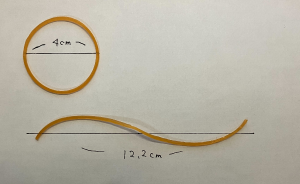
手元で実測してみたら円周率＝12.2 / 4.0 ≒ 3.1でした。（輪ゴムで測ったのは若干悪手でした。）

さあ、そろそろパソコンの出番が近づいてきました。がもう少し準備が必要です。

円を多角形で挟み込む

こんな感じで円に内接する4角形と円に外接する4角形を描いてみます。

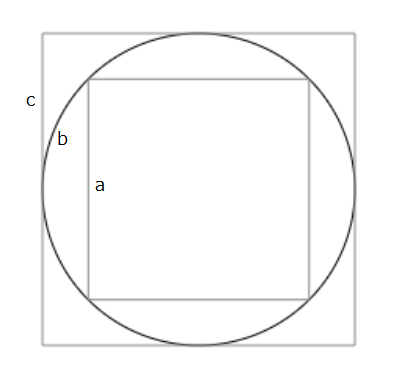
この図を見ると、
a.内接する四角形の周
b.円の周
c.外接する四角形の周
としたときに、
a < b < c
となっているように見えます。
となると、aとcを求めることで、bがどの範囲にあるかを確定させることができそうです。

そして、それに成功したら、6角形、10角形、、、、とN角形のNを増やしていくことで、よりbの値を精緻に範囲確定ができるように思われます。

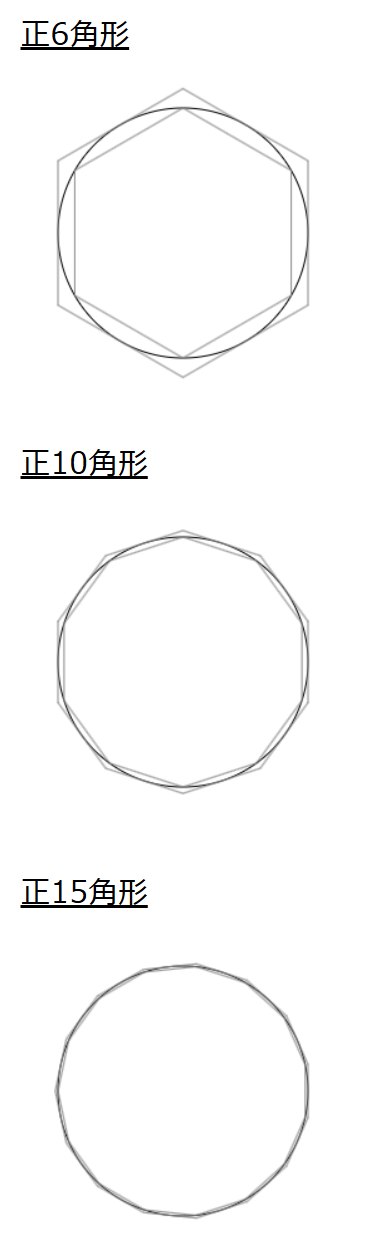
実際、15角形あたりですでにほとんど円と同じような値になりそうです。

ですが私は以下の２つの理由で、このアプローチを諦めました。

理由1：sin/cosが難しい

多角形の周を求めるのには、sinかcosを使わねばならなそうで、これは今回難しいことはやらないという前提に反します。
実際、sin/cosを使うと計算がパソコンの電卓機能任せになってしまうのでダメですね。

理由2：a < bはOK。だけどb < cは本当？

改めて上の図を見るに、a < bは直線の性質的にまあそうだろうという気がするのですが、b < cは、たぶんそうだろうけど本当？というところがうまく説明することができませんでした。100%そうだろうと確信できないものを使うのはちょっと気持ち悪いので、やめましょう。

アプローチを変更して面積の公式を使ってみる

そこで、もう一つの公式である、
②円の面積＝半径 x 半径 x 円周率
を使ってみましょう。

この公式はどのように証明できるのでしょうか。実はこれは結構簡単です。
円をピザに見立てて半分に切ってみましょう。そして2つのピザを、中心が上になるように横並びにするとこんな感じになります。

それでは2枚ではなく4枚、8枚、32枚…とより細かく切り分けてみましょう。

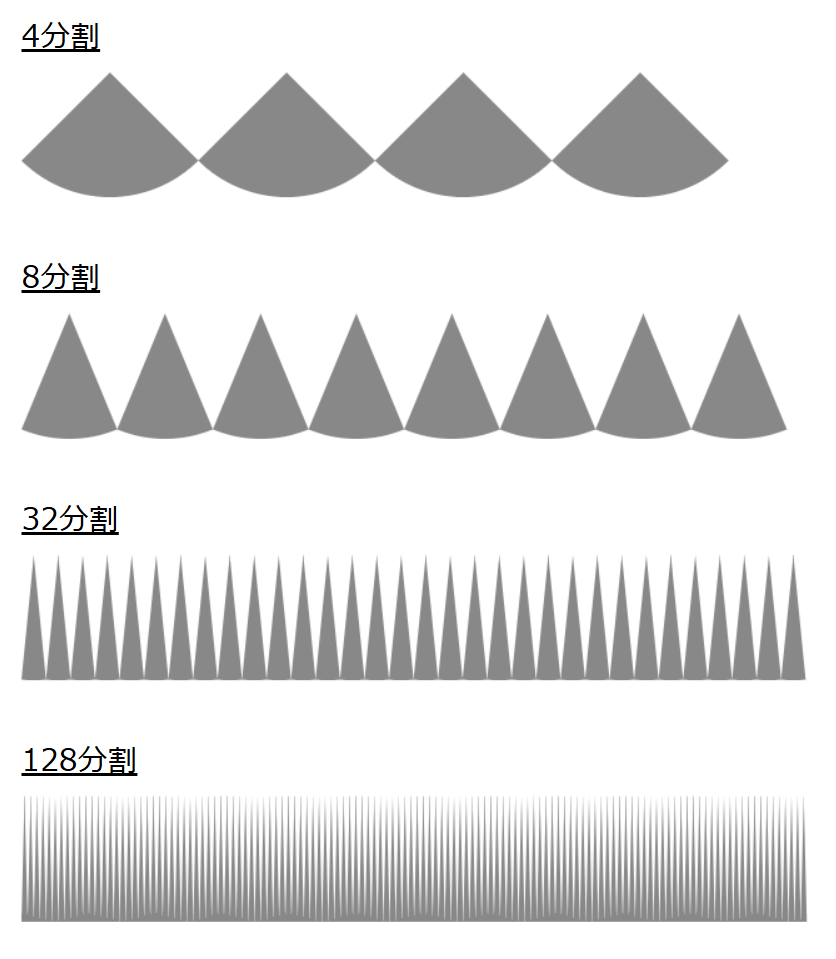
そうすると最終的に、これらはとても底辺の小さい縦長の細い三角形を横に並べたものとみなせる状態になりました。
無限に細かく分割すると、
・三角形はすべて高さが円の半径とほぼ等しく、
・すべての三角形の底辺の和は元の円の円周とほぼ一致する
と考えてよいでしょう。

そのため、元の円の面積は、
S = (三角形の底辺の和) x (三角形の高さ) x 1/2
   ≒ 円周 x 円の半径 x 1/2
   = (円の半径 x 2 x π) x 円の半径 x 1/2
   = 円の半径 x 円の半径 x π
となります。

これで円の面積に関する公式がほぼ証明されました。

ここからはこの公式が使えますので、さきほどの内接する四角形と外接する四角形で考えますと、
内接する四角形の面積 < 円の面積 < 外接する四角形の面積
という不等式で挟み込むことでπの値を範囲確定できそうです。

というのも、
円の面積 = 円の半径 x 円の半径 x π
ですので、

内接する四角形の面積 / (円の半径)² < π < 外接する四角形の面積 / (円の半径)²

と表すことができるからです。
πの左側も右側も計算で出せそうですね。

さあ、とうとうPCの出番です

やっと方針が決まってまいりました。

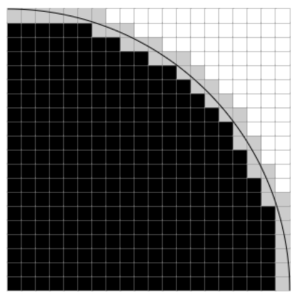
ところで、円は扇形としてはぐるっと360度回した形になっていて、xy平面の中央に置くと、上下・左右で線対称のため、全体を計算するのはやや冗長です。
第一象限（右上部分）だけで考えてみることで計算量を省いてみましょう。

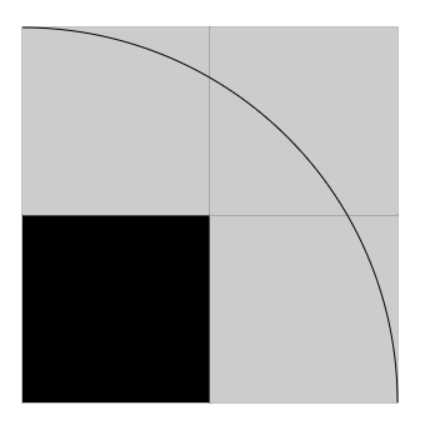
この図で考えますと、
黒い正方形の面積の和 < 円(の一部)の面積 < 黒とグレーの四角形の面積の和
となり、円の半径を1とすると、
1/4 < (1x1xπ)/4 < 4/4となり、
すなわち1 < π < 4 ということがわかりました！
なんてことでしょう、素晴らしい、great!!

しかしちょっと精度がいまいちですね。ここから精度を上げていくのにはPCが役に立ちます。
上記の例では、面積1の正方形を2×2分割しました。これを4×4分割、8×8分割…N x N分割と増やしていくことで、より精度をあげていくことができそうです。

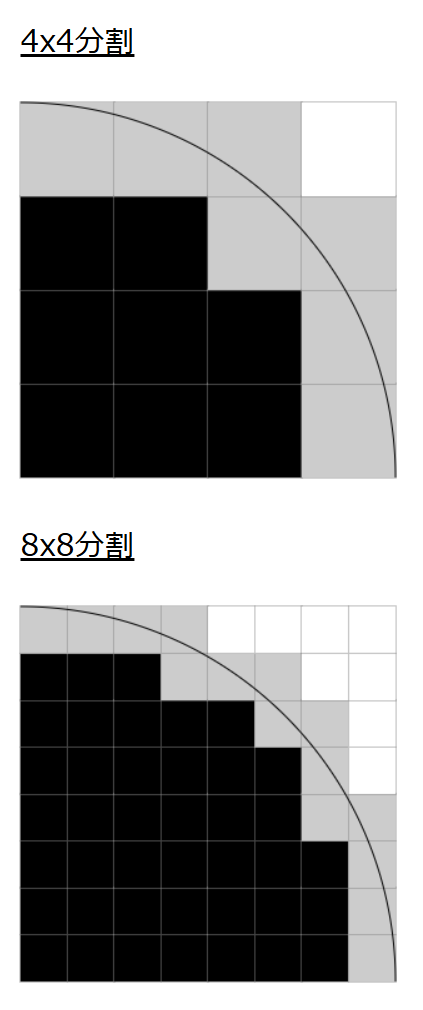
つまり、分割数Ｎを引数として渡すことで、πの範囲を自動計算してくれるプログラムを書けばよいわけですね。

ということで、Nを渡すことで範囲を返してくれる関数を書いてみましょう。
プログラムとしてはこんな感じです。（自分で書いてみたほうが楽しいのでリンクにしておきます。）

このプログラムでは、分割された四角形それぞれについて、
・完全に円内に含まれる（黒）
・一部が円に含まれる（グレー）
・完全に円の外にある（白）
の３種類の判定をしています。

判定方法としては、分割された各々の正方形の左下と右上の角の点について、原点0からの距離が1未満か1以上かで判定しています。

そして各点の原点からの距離は三平方の定理を利用しています。
三平方の定理は証明しなくてよいのかですって？そろそろ疲れてきたので、それは以下の図を見て証明済みとしてください。

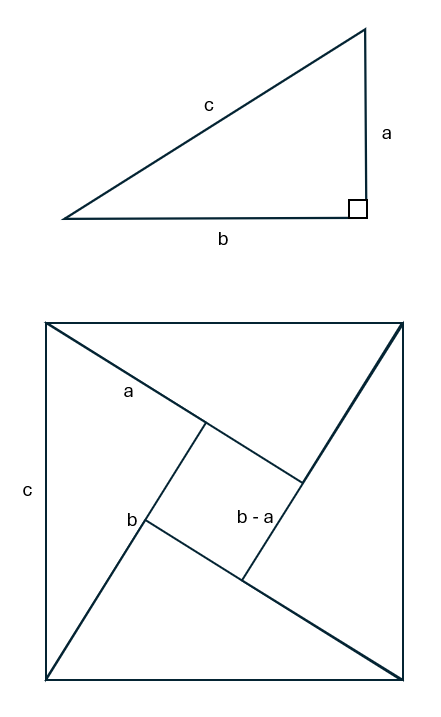
大きい四角形の面積 = c²
三角形４つの面積 = a x b x 1/2 x 4 = 2ab
真ん中の小さい面積 = (a-b)²
よって、
c² = 2ab + (a-b)²   
       = 2ab + a² -2ab + b²     
       = a² + b²
ふー。

で、気になる結果はというと

さて、さきほど完成したプログラムにて、N=10,000を渡すと、

3.1411904448442 < pi < 3.1419902448482

と絞ることできました。
我々のよく知っている、3.14までは確実に正しそうですね！
これが本日到達したかったゴールとなります！おめでとう！！

かくして私たちは無事、紙とペンと算数とパソコンだけを使って、円周率πの値を求めることができました。ルートとか三角比とかが分からなくてもここまで辿り着くことができました。感無量です。

プログラムの飽くなき最適化

ちなみに、もっと高い精度を求めてＮ=100,000の値を入れると、１分以内に計算が終了しませんでした。
現在πの桁数は100兆桁以上の精度で求められているようですので、これではまだまだ赤子のようなプログラムですね。

これをどう改修していくかは時としてプログラムをチューニングすることで解決し、時として方針そのものの変更が必要になるのですが、まだ簡単にチューニングの余地がありますので、改善点をあげて締めとしましょう。

先ほどの黒と白の四角形についてはすでに円内あるいは円外にあることが確定していますので、それらの四角形をより細かく分割して計算することは単に計算の無駄となります。
ですので、中途半場なグレーの四角形のみをより細かく計算するというプログラムに改修することで精度を高められそうですね。

これは面白い試みですので、あとは興味があればご自身でやってみましょう。要望があればコラムの続きを書きます。

今回は天下りを極力排して一歩ずつ進めたので骨が折れましたが、プログラムの力を少しでも実感していただけたら嬉しいです。
ついでに数学が嫌いな人が「数学ってちょっと面白いかも」と…、いやそれはちょっと望みすぎですね。

編集後記：本体のプログラムよりも、挿絵の描画を行うプログラムを書く方がはるかに時間がかかりました。。